Contents |
|
About this site |
|
Download the Cyclopedia |
|
Awards |
|
Links | |

|
|
Troy Weight is used by jewellers and at the Mint. Its denominations are the pound, lb., = 12 ounces = 5,760 grains; ounce, oz., = 480 grains; and pennyweight, dwt., = 24 grains.
Apothecaries' Weight is used in prescribing and dispensing medicines, and in chemical and pharmaceutical operations generally. It is the official standard of the U. S. Pharmacopoeia. The British Pharmacopoeia uses the avoirdupois pound and ounce; hence the two agree only in the grain measure. The denominations of apothecaries' weight are the pound, lb, = 12 ounces = 5,760 grains; the ounce, oj, = 8 drachms = 480 grains; the drachm, dj, = 3 scruples = 60 grains; the scruple, sj, = 20 grains; and the grain, gr.
Avoirdupois Weight is the commercial weight, and is generally employed in the receipts in this volume. Its pound, lb., = 16 ounces, oz., = 7,000 grains. The ounce contains 437.5 grains. The apothecaries' or troy ounce contains 42 1/2 grains more than the avoirdupois ounce, and the apothecaries or troy pound contains 1.240 grains less than the commercial or avoirdupois pound. The troy pound contains 12 oz., the avoirdupois 16 oz.
Useful in determining the troy weight of silver by ordinary weights.
1 lb. troy = 0.822857 lb. av. = 13 oz. 72.5 grs.
1 lb. avoirdupois = 1.215277 lb. troy = 1 lb. 2 oz. 280 grs.
Are convenient standards of weight. Those of gold are to be preferred, and when new will rarely be found to vary more than the tenth of a grain from the following weights:
| Double eagle, | $20, | weighs | 516 | grs. |
| Eagle, | $10, | " | 258 | " |
| Half eagle, | $5, | " | 129 | " |
| Quarter eagle, | $2 50, | " | 64 1/2 | " |
| Three dollar, | $3, | " | 77.4 | " |
| One dollar, | $1, | " | 25.8 | " |
In the United States the old wine gallon (Cong.), of 231 cubic inches = 58,328.8 grains of water at 60°, is used. In England the Imperial gallon of 277.274 cubic inches = 70,000 grains = 10 lb. av. is used. The minim of the former = 0.95 gr., of the latter= 0.91 gr. The former contains 16 fluidounces to the pint (O.), the latter 20. The following tables give the value of each in grains of pure water, at 60°.
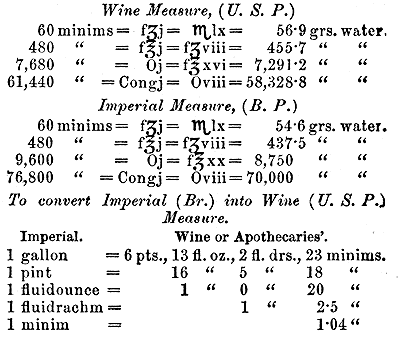
Adopted in France and on the Continent, is used in this country in scientific research. The standard of length is the metre (1/10,000,000 of a quadrant of the earth's meridian), which is equal (as corrected by Prof. Bache) to 39.36850535 inches, or, roughly, about 3 1/4 feet. This, as well as the measures of capacity and weight, is increased or divided decimally. The prefixes are deca (10 times), hecto (100 times), kilo ( 1000 times), and myria (10,000 times); deci (1/10), centi (1/100), milli (1/1000). The kilometre is equal to about two-thirds of a mile.
The cubic decimetre is the unit of capacity, and is called a litre, and is equal to 1.765 imperial pints, or 2.1135 wine pints (the latter are used in the United States). The weight of 1 litre of water at 39.10°, is called a kilogramme, and that of a millilitre of water a gramme = 15.434 grains. The kilogramme is rather less than 2 1/4 lbs. avoirdupois. The metrical pound of France is half a kilogramme. One fluidounce equals in capacity 29.53 cubic centimetres.
| Name. | Equivalent in Grammes. | Equivalent in Grains. | Equivalent in Avoirdupois. | Equivalent in Apothecaries' Weight, (U.S.P.) |
Milligramme = Centigramme = Decigramme = Gramme = Decagramme = Hectogramme = Kilogramme* = Myriagramme = |
.001
.01
.1
1.
10.
100.
1,000.
10,000. |
.0154
.1543
1.5434
15.434
154.3402
1543.4023
15434.0234
154340.2344 |
lb. oz. gr.
0 1/4 .45
3 1/2 12.152
2 3 1/4 12.173
22 0 3/4 12.
|
lb. oz. dr. gr.
1.5
15.4
2 34.0
3 1 43.0
2 8 1 14.
26 9 4 20.
|
| Eng. Cubic Inches. | Apothecaries' or Wine Measures. | |
| Millilitre | 0.061028 | = 16.2318 minims. |
| Centilitre | 0.610280 | = 2.7053 fluidrachms. |
| Decilitre | 6.102800 | = 3.3816 fluidounces. |
| Litre | 61.028000 | = 2.1135 pints. |
| Decalitre | 610.280000 | = 2.6419 gallons. |
| Hectolitre | 6102.800000 | |
| Kilolitre | 61028.000000 |
1 litre = 0.22017 galls., 0.88066 qts., 1.76133 pts. Stere (cubic metre) = 220.16643 galls.
A box 20 inches square, and 16 1/8 inches deep, will contain 1 barrel (3 bushels).
A box 15 inches square, and 14 1/3 inches deep will contain half a barrel.
A box 17 inches by 14 inches, and 9 inches deep, will contain 1 bushel.
A box 10 inches by 12 inches, and 9 inches deep, will contain half a bushel.
A box 8 inches square, and 8 3/8 inches deep, will contain 1 peck.
A box 8 inches square, and 4 3/16 inches deep, will contain 1 gallon (dry) = 1/8 bushel = 268 3/4 cubic inches.
A box 4 inches square, and 4 3/32 inches deep, will contain 1 quart
12 inches = 1 foot.
3 feet = 1 yard.
1 mile = 1760 yards = 5280 feet = 63,360 inches.
|
|
|
|
1. In a right-angled triangle the sum of the squares of the two shorter sides = the square of the hypothenuse: the square of the hypothenuse less the square of one side = the square of the third side.
2. The diameter of a circle X 3.1416 = the circumference.
3. The circumference of a circle X 0.31831 = the diameter.
4. Given a chord and versed sine -- to find the diameter of the circle. Divide the square of half the chord by the versed sine, and add the versed sine to the product = the diameter.
5. To find the length of an arc of a circle, when the cord of the whole arc and the chord of one half of the arc are known, from 8 times the chord of one-half the arc, subtract the chord of the whole arc: one-third of the remainder will be the length of the arc nearly.
6. Periphery of an elipse. Multiply the square root of the sum of the squares of the axes by 2.22.
Areas. - Product of two Linear Dimensions (proportioned to the squares of similar sides).
9 square feet = 1 square yard.
Acre = 43,560 square feet = 4480 yards = (660 X 66 feet).
Square mile = 640 acres.
1. Parallelogram (squares rectangular or rhomboidal) = the product of the length of one side X by perpendicular height.
2. Triangle = product of base X by one-half the perpendicular height.
3. Triangle - Area from 3 sides given. From the half sum of the three sides subtract each side separately; multiply the half sum and the three remainders together, and the square root of the product will be the area.
4. Trapezoid = the sum of the two parallel sides X by half the perpendicular height.
5. Circle = the square of the diameter X 0.7854, or square of the circumference X 0.07958.
6. Sector of a Circle = radius of the circle X by onehalf the arc of the sector.
7. Segment of a Circle. - Find the area of a sector of a circle having the same arc, and deduct the triangle formed between the two radii and the chord of the arc.
| 8. Cube. 9. Parallelopipidon. 10. Prism. |
} = { |
Sum of area of sides and bases. |
11. Cylinder = circumference of base X height + area of bases.
| 12. Cone. 13. Pyramid. |
} = { |
Circumference of bases X one-half slant height + area of base. |
Sphere = square of diameter X 3.1416.
French square metre, 1550.85 square inches = 10.7698 square feet.
Cubic Content. - Product of three Linear Dimensions (proportional to cube of similar sides).
| Cubic foot | = | 1,728 | cubic in. | |||
| Cubic yard | = | 27 | cubic ft. | = | 46,656 | " |
| Barrel | = | 4.8125 | " | = | 8,316 | " |
| Bushel | = | 1.2438 | " | = | 2,150 | " |
| Gallon (wine) | = | 231 | " |
Ton = 2240 lbs. avoirdupois.
1 gallon of water weighs 58,328.8 grains troy = 10.126 lbs. troy.
| Cylindrical | inches | X | .0004546 | = | cubic | feet. |
| " | feet | X | .02909 | = | " | yards. |
| Cubic | inches | X | .00058 | = | " | feet. |
| " | feet | X | .03704 | = | " | yards. |
| " | feet | X | 7.48 | = | U. S. States | gallon. |
| " | inches | X | .0004329 | = | " | " |
| Cylindrical | feet | X | 5.874 | = | " | " |
| " | inches | X | .0034 | = | " | " |
Contents of Casks. - Add into one sum 39 times the square of the bung diameter, 25 times the square of the head diameter, and 26 times the product of the two diameters; then multiply the sum by the length, and the product again by 24/2 for wine gallons.
Let A and B be areas of ends of solids, and C the area of a section parallel to, and equidistant from the ends, and L the distance between the ends:
| A + B + 4 C | ||
| Solidity = | X L. |
1. Cube = side X side X side, or = area of base X perpendicular height.
2.
| Parallelopipidon Prism Cylinder |
} = { |
Area of base X by perpendicular height. |
3.
| Cone Pyramid |
} = { |
Area of base X by 1/3 the perpendicular height. |
4. Frustrum of Cone or Pyramid = sum of the areas of the two ends + the square root of their product X by 1/3 of the perpendicular height.
5. Sphere = cube of the diameter X 0.5236.
6. Spherical Segment = 3 times the square of the radius of its base + the square of its height X the height X 0.5s36.
1. Perch, Masons' or Quarrymen's Measure.
| 16 1/2 feet long, 16 inches wide, 12 inches high. |
} = { |
22 cubic feet. To be measured in wall. |
| 16 1/2 feet long, 18 inches wide, 12 inches high. |
} = { |
24.75 cubic feet. To be measured in pile. |
1 cubic yard = 3 feet X 3 feet X 3 feet = 27 cubic feet.
The cubic yard has become the standard for all contract work of late years.
Stone walls less than 16 inches thick count as if 16 inches thick to mason; over 16 inches thick each inch additional is measured.
|
|
||||||||||||||||||||||||||||||||||||
Cubic yard = 600 bricks in wall.
Perch (22 cubic feet) = 500 bricks in wall.
To pave 1 sq. yard on flat requires 41 bricks.
To pave 1 sq. yard on edge requires 68 bricks.
Boards are sold by superficial measure at so much per foot of 1 inch or less in thickness, adding one-fourth to the price for each quarter-inch thickness over an inch.
In ordinary language the terms density and specific gravity (s. g.) are used to represent the relative weights of equal bulks or volumes of different substances. In order to compare these conveniently, pure water at 60° is taken as the standard. A cubic foot of water weighs 100 oz., hence to determine the weight of a given bulk of any body the specific gravity of which is known, multiply the cubic content in feet by 1000, and this by the s. g., and the product will be the weight in ounces avoirdupois. Thus, the s. g. of cast-iron is 7.207, that is, it is 7.207 times heavier than an equal bulk of water. A cylinder of cast-iron 1 foot in diameter and 10 feet high, would contain 10 cubic feet, 10 X 1000 X 7.207 = 72.070 oz. = 4500 lbs.
1. By the Pitcher. - Fill a pitcher, or similar vessel, brim full; put in the body; it will displace its own bulk of water; catch this water as it overflows and weigh it. Divide the weight of the body by that of the water displaced, the quotient will be its specific gravity. A very neat instrument for performing this process accurately has been contrived by Messrs. Eckfeldt and Dubois, of the United States Mint.
2. By the Hydrostatic Balance. - Weigh the body, fasten it, preferably by a horse-hair, immerse it in water, and note the loss of weight. The weight in air divided by the loss of weight in water = the s. g.
3. When the Body is Lighter than Water. - Attach to it some heavy body of known weight in air and water. Weigh the two together, first in air and then in water, note the loss. The loss of weight of the heavy body in water being known the difference between these losses divided into the weight of the light body in air, will give the specific gravity. Thus, a bit of wood weighed in air 200 grains, attached to a piece of copper the two weighed in air 2247 grains, and in water 1620 grains suffering a loss of 627 grains, the copper alone loses in water 230 grains, 627 - 230 = 397, the loss of the wood; 200/397 = 0.504, s. g. of the wood.
Take its s. g. in regard to some liquid which does not dissolve it, multiply this by the s. g. of the liquid.
Thus, a piece of sugar weighed in air 400 grs. it lost in oil of turpentine 217.5. 400/217.5 = 1.84. The s. g. of turpentine is .87; 1.84 X .87 = 1.6., s. g. of the sugar.
Introduce it into a counterpoise bottle, of which the capacity is known. Fill the bottle with pure water at 60°. It will hold as much less as is equal to the bulk of the powder, and the weight of the powder in air divided by this difference will give the s. g.
Thus, the bottle holds 1000 grs. of water, 100 grs. of emery are introduced, and the bottle filled up with water. If no water were displaced the two should weigh 1100 grs., they really weigh 1070; the difference, 30 grs. = the weight of water displaced; 100/30 = 3.333, s. g of the emery.
As a nugget of gold and quartz. Take the s. g. of the nugget, that of gold and quartz being known, then apply the following formulae:
| s. g. nugget - s. g. quartz s. g. gold -s. g. quartz |
X | s. g. gold s. g. nugget |
X weight of nugget
| s. g. gold - s. g. nugget s. g. gold -s. g. quartz |
X | s. g. quartz s. g. nugget |
X weight of nugget
This method will do approximately, but not accurately for alloys of metals generally.
Take a bit of glass rod, note its loss when weighed in water and in the liquid under trial. Divide the latter by the former, the quotient will be the s. g. of the liquid. Thus a glass rod loses in water 171 grs., in alcohol, 143 grs. 143/171 = .836. s. g. of the alcohol.
These are made to hold 100 or 1000 grs. of pure water at 60°, and are accompanied by a counterpoise. It is only necessary to fill the bottle with the liquid to be tested. Counterpoise and weigh; the weight in grains will be the s. g. Oily and viscous matter should never be introduced into the s. g. bottle. In case the s. g. bottle is not at hand any light flask will do. Make a file mark on the neck, counterpoise it, fill to the mark with pure water at 60, note the weight of the water. Empty, dry thoroughly and fill with the liquid to be tested; the weight of this divided by that of the water = s. g.
Are instruments for determining the specific gravity of liquids by noting the depth to which a stem sinks. They consist of a cylinder with a weight beneath it to make it float upright, and a graduated stem. When intended for liquids lighter than water, the 0 or point at which they float in pure water at 60° is at the lower point of the stem, and as the liquid is lighter they sink more deeply; for liquids heavier than water the 0 is at the top of the scale. Many are graduated according to their proposed use, as alcoholometers, lactometers, sacharometers. (see DISTILLATION). The graduation most employed is that of Beaume. Excellent hydrometers with the degrees and the true s. g. on the same stem are made by Dr. W. H. Pile of Philadelphia.
1. For liquids heavier than water - Subtract the degree B. from 145, and divide into 145, the quotient is the s. g.
2. For liquids lighter than water - Add the degree B. to 130, and divide it into 140. The quotient is the s. g.
1. For liquids heavier than water. - Divide the s. g. into 145, and subtract from 145. The remainder is the degree B.
2. For liquids lighter than water. - Divide the s. g. into 140 and subtract 130 from the quotient. The remainder will be the degree B.
| Mercury | 13,600 |
| Lead | 11,325 |
| Copper | 9,000 |
| Cast Brass | 8,000 |
| Steel | 7,850 |
| Wrought Iron | 7,780 |
| Cast Iron | 7,207 |
| Tin | 7,300 |
| Marble | 2,690 |
| Common Stone | 2,520 |
| Brick | 2,000 |
| Soil | 1,974 |
| Coal, anthracite | 1,640 |
| Coal, bituminous | 1,270 |
| Sand | 1,620 |
| Sea-water | 1,030 |
| COMMON WATER | 1,000 |
| Oak, (dry) | 925 |
| Ash | 800 |
| Maple | 755 |
| Elm | 600 |
| Yellow Pine | 660 |
| White Pine | 554 |
| Cork | 249 |
| Carb. Acid | 1.9 |
| Air | 1.25 |
| Coal Gas | 0.6 |
| Hydrogen | 0.0848 |
The specific gravity in table also represents the number of ounces in each substance in 1 cubic foot / 16 = lbs.
| 1 | cubic foot of | Cast Iron | = | 450 | lbs. |
| 1 | " | White Pine | = | 34.6 | " |
| 1 | " | Water | = | 62.5 | " |
| 10.9 | " | Air | = | 1 | " |
| 22 | " | Coal Gas | = | 1 | " |

The figures on the index at the right hand denote even hundreds. When the hand completes the entire circle it denotes ten hundred, and is registered by the hand in the centre circle, pointing to one - each figure in the centre circle being a thousand - this entire circle being ten thousand is registered on the index of the left hand circle by the hand, there denoting by each figure, ten thousand.
The quantity of gas which passes through the meter, is ascertained by reading from the index at the time the amount is required to be known and deducting therefrom the quantity shown bythe index at a previous observation.
If the whole is registered by the hands on the three circles above, it indicates; 49,900
Amount at previous observation, as shown by the dotted lines; 42,500
Shows amount which passed through since last taken off; 7,400
The register at all times shows the quantity that has passed through since the meter was first set, by deducting from which the amount that has been paid for (without any regard to the time when), shows that the difference remains unpaid.
Turn the gas partly off at the meter; much gas is burned to waste by too great pressure in certain localities. In buildings of any size a good regulator will soon pay for itself. Cresson's is the best.
The following are those in common use:
Batswing. - This has a single slit at the top of the burner. It is very steady, does not change its form under any pressure. It is, therefore, used in street lamps. It is not, however, economical.
Fish-tail. - This form is generally used in houses; it has two openings in the top, from which the jets of gas issue and form a flat flame, the plane of which is at right angles to that of the openings. When the pressure is too great the flame elongates and sings, thus calling attention to the waste. It is an economical burner, but flickers. This unsteadiness is trying to the eyes, and the fish-tail should never be used to read or write by.
Argand. - These are the steadiest and most economical burners, but require a chimney. The gas is allowed to escape by a ring of holes, and the air is admitted both inside and outside of this ring. In the patent Argand the outer ring of air passes through a series of small openings, and the inner ring is deflected into the flame by a button; It requires a swelled chimney. By cutting off the button a steadier light is obtained, and the economy is nearly the same; straight chimneys are more easily obtained than the others. The best flint-glass chimneys are in the end the cheapest; great loss of light ensues if they are not kept clean. But putting a chimney into hydrant-water, and gradually heating it, it may be cleaned safely; paper gives the best finish. The larger the burner the greater the relative economy.
| Batswing | consuming 5 feet, | 1.000 |
| Large patent Argand burner | consuming 6 feet, | 2.880 |
| Common Argand | consuming 5.4 feet, | 2.132 |
| Single jet | consuming 2.2 feet, | 1.191 |
| Fish-tail (Union jet) | consuming 4.5 feet, | 1.513 |
| Large Batswing | consuming 11.3 feet, | 2.03 |
| Wax candle, 4 to lb. | 0.143 | |
| Sperm candle, 6 to lb. | 0.111 | |
| Tallow candle, 5 to lb. | 0.1 |
| 1 wax candle, | 4 to a lb. | burns 13 hours. |
| 1 spermaceti candle, | 6 to a lb. | burns 8 hours. |
| 1 Tallow candle, | 6 to a lb. | burns 6 hours. |
Explanatory Remarks.
The first column embraces the names of the countries where the coins are issued, the second contains the names of the coin, only the principal denominations being given. The other sizes are proportional; and when this is not the case, the deviation is stated.
The third column expresses the weight of a single piece in fractions of the Troyounce, carried to the thousandth, and in a few cases to the ten thousandth, of an ounce. The method is preferable to expressing the weight in grains for commercial purposes, and corresponds better with the terms of the Mint. It may be readily transferred to weight in grains by the following rule: Remove the decimal point, from one-half deduct four per cent. of that half, and the remainder will be grains.
The fourth column expresses the fineness in thousands, i. e., the number of parts of pure gold or silver in 1000 parts of the coin.
The fifth column expresses the valuation of coin. The value of silver fluctuates.
| Country. | Denominations. | Weight. Oz. Dec. |
Fineness. Thous. |
Value. 1864. |
| Australia | Pound of 1852 | 0.281 | 916.5 | $ 5.32.37 |
| " | Sovereign, 1855-60 | 0.256.5 | 916 | 4.85.58 |
| Austria | Ducat | 0.112 | 986 | 2.28.28 |
| " | Souverain | 0.363 | 900 | 6.75.35 |
| " | New Union Crown (assumed) | 0.357 | 900 | 6.64.19 |
| Belgium | Twenty-five Francs | 0.254 | 899 | 4.72.03 |
| Bolivia | Doubloon | 0.867 | 870 | 15.59.25 |
| Brazil | Twenty Milreis | 0.575 | 917.5 | 10.90.57 |
| Central America | Two Escudos | 0.209 | 853.5 | 3.68.75 |
| Chili | Old Doubloon | 0.867 | 870 | 15.59.26 |
| " | Ten Pesos | 0.492 | 900 | 9.15.35 |
| Denmark | Ten Thaler | 0.427 | 895 | 7.90.01 |
| Ecuador | Four Escudos | 0.433 | 844 | 7.55.46 |
| England | Pound or Sovereign, new | 0.256.7 | 916.5 | 4.86.34 |
| " | Pound or Sovereign, average | 0.256.2 | 916 | 4.84.92 |
| France | Twenty Francs, new | 0.207.5 | 899.5 | 3.85.83 |
| " | Twenty Francs, average | 0.207 | 899 | 3.84.69 |
| Germany, North | Ten Thaler | 0.427 | 995 | 7.90.01 |
| " | Ten Thaler, Prussian | 0.427 | 903 | 7.97.07 |
| " | Krone (Crown) | 0.357 | 900 | 6.64.20 |
| Germany, South | Ducat | 0.112 | 986 | 2.28.28 |
| Greece | Twenty Drachms | 0.185 | 900 | 3.44.19 |
| Hindostan | Mohur | 0.374 | 916 | 7.08.18 |
| Italy | Twenty Lire | 0.207 | 898 | 3.84.27 |
| Japan | Old Cobang | 0.362 | 568 | 4.44.0 |
| " | New Cobang | 0.289 | 572 | 3.57.6 |
| Mexico | Doubloon, average | 0.867.5 | 866 | 15.52.98 |
| " | Doubloon, new | 0.867.5 | 870.5 | 15.61.05 |
| Naples | Six Ducati, new | 0.245 | 996 | 5.04.43 |
| Netherland | Ten Guilders | 0.215 | 899 | 3.99.56 |
| New Granada | Old Doubloon, Bogota | 0.868 | 870 | 15.61.06 |
| " | Old Doubloon, Popayan | 0.867 | 858 | 15.37.75 |
| " | Ten Pesos new | 0.525 | 891.5 | 9.67.51 |
| Peru | Old Doubloon | 0.867 | 868 | 15.55.67 |
| Portugal | Gold Crown | 0.308 | 912 | 5.80.66 |
| Prussia | New Union Crown (assumed) | 0.357 | 900 | 6.64.19 |
| Rome | Two and a half Scudi, new | 0.140 | 900 | 2.60.47 |
| Russia | Five Roubles | 0.210 | 916 | 3.97.64 |
| Spain | One Hundred Reals | 0.268 | 896 | 4.96.39 |
| " | Eighty Reals | 0.215 | 869.5 | 3.86.44 |
| Sweden | Ducat | 0.111 | 975 | 2.23.72 |
| Tunis | Twenty-five Piastres | 0.161 | 900 | 2.99.54 |
| Turkey | One Hundred Piastres | 0.231 | 915 | 4.36.93 |
| Tuscany | Sequin | 0.112 | 999 | 2.31.29 |
| Country. | Denominations. | Weight. Oz. Dec. |
Fineness. Thous. |
Value. 1864. |
| Austria | Old Rix Dollar | 0.902 | 833 | $ 1.02.27 |
| " | Old Scudo | 0.836 | 902 | 1.02.64 |
| " | Florin before 1858 | 0.451 | 833 | 51.14 |
| " | New Florin | 0.397 | 900 | 48.63 |
| " | New Union Dollar | 0.596 | 900 | 73.01 |
| " | Maria Theresa Dollar, 1780 | 0.895 | 838 | 1.02.12 |
| Belgium | Five Francs | 0.803 | 897 | 98.04 |
| Bolivia | New Dollar | 0.643 | 903.5 | 79.07 |
| " | Half Dollar | 0.432 | 667 | 39.22 |
| Brazil | Double Milreis | 0.820 | 918.5 | 1.02.53 |
| Canada | Twenty Cents | 0.150 | 925 | 18.87 |
| Central America | Dollar | 0.866 | 850 | 1.00.19 |
| Chili | Old Dollar | 0.864 | 908 | 1.06.79 |
| " | New Dollar | 0.801 | 900.5 | 98.17 |
| Denmark | Two Rigsdaler | 0.927 | 877 | 1.10.65 |
| England | Shilling, new | 0.182.5 | 924.5 | 22.96 |
| " | Shilling, average | 0.178 | 925 | 22.41 |
| France | Five Francs, average | 0.800 | 900 | 98.00 |
| Germany, North | Thaler, before 1857 | 0.712 | 750 | 72.67 |
| " | New Thaler | 0.595 | 900 | 72.89 |
| Germany, South | Florin, before 1857 | 0.340 | 900 | 41.65 |
| " | New Florin (assumed) | 0.340 | 900 | 41.65 |
| Greece | Five Drachms | 0.719 | 900 | 88.08 |
| Hindostan | Rupee | 0.374 | 916 | 46.62 |
| Japan | Itzebu | 0.279 | 991 | 37.63 |
| " | New Itzebu | 0.279 | 890 | 33.80 |
| Mexico | Dollar, new | 0.867.5 | 903 | 1.06.62 |
| " | Dollar, average | 0.866 | 901 | 1.06.20 |
| Naples | Scudo | 0.844 | 830 | 95.34 |
| Netherlands | Two and a half Guild | 0.804 | 944 | 1.03.31 |
| Norway | Specie Daler | 0.927 | 877 | 1.10.65 |
| New Granada | Dollar of 1857 | 0.803 | 896 | 97.92 |
| Peru | Old Dollar | 0.866 | 901 | 1.06.20 |
| " | Dollar of 1858 | 0.766 | 909 | 94.77 |
| " | Half Dollar, 1835 - '38 | 0.433 | 650 | 38.31 |
| Prussia | Thaler before 1857 | 0.712 | 750 | 72.68 |
| " | New Thaler | 0.595 | 900 | 72.89 |
| Rome | Scudo | 0.864 | 900 | 1.05.84 |
| Russia | Rouble | 0.667 | 875 | 79.44 |
| Sardinia | Five Lire | 0.800 | 900 | 98.00 |
| Spain | New Pistareen | 0.166 | 899 | 20.31 |
| Sweden | Rix Dollar | 1.092 | 750 | 1.11.48 |
| Switzerland | Two Francs | 0.323 | 899 | 39.52 |
| Tunis | Five Piastres | 0.511 | 898.5 | 62.49 |
| Turkey | Twenty Piastres | 0.770 | 830 | 86.98 |
| Tuscany | Florin | 0.220 | 925 | 27.60 |
|